Magic Square
K Subramani
International Institute of Information Technology, Bangalore
Email : Subramani.k@iiitb.ac.in
A magic square is a special arrangement of numbers in a square grid. It typically uses whole numbers, one in each cell, and has a specific size denoted by “n x n” (where n represents the number of rows and columns). The magic lies in how the numbers are placed. In a perfect magic square, the sum of the numbers in each row, each column, and along both main diagonals will all be equal. This special sum is called the magic constant. The main diagonals run diagonally from corner to corner, and for reference, an image can be found online to visualize this,
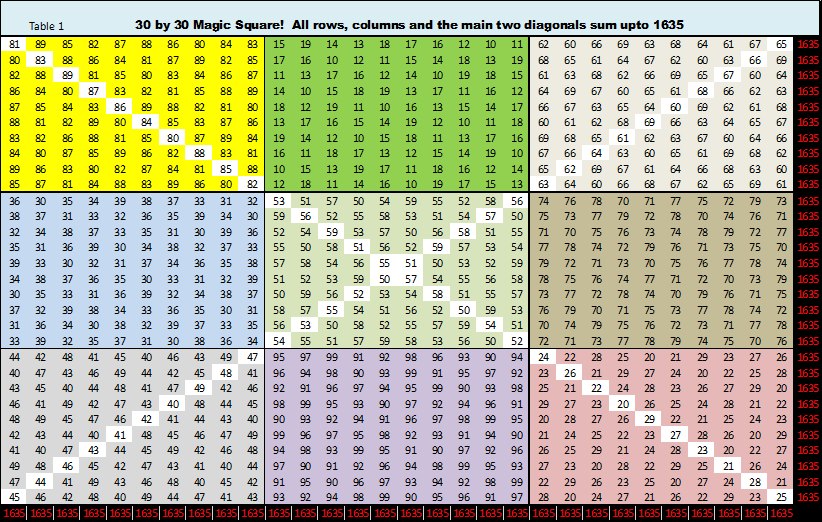
For a 30 x 30 square, even after converting single digits to double digits, you’d end up with numbers from 10 to 89. Arranging these numbers to satisfy the magic square properties (equal sums in rows, columns, and diagonals) is mathematically difficult.
However, there are techniques to construct special magic squares for even dimensions like 30 x 30. These squares might not have all the properties of a traditional magic square but can achieve some level of magic, like specific sums along certain lines or regions
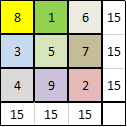
Intuition: Inspired from 3 by 3 Magic square, we converted every single digit into double digit.
i.e., we suffixed 0,1,2,3,4,5,6,7,8 & 9 to the number 8
now it becomes 80,81,82,83,84,85,86,87,88 & 89
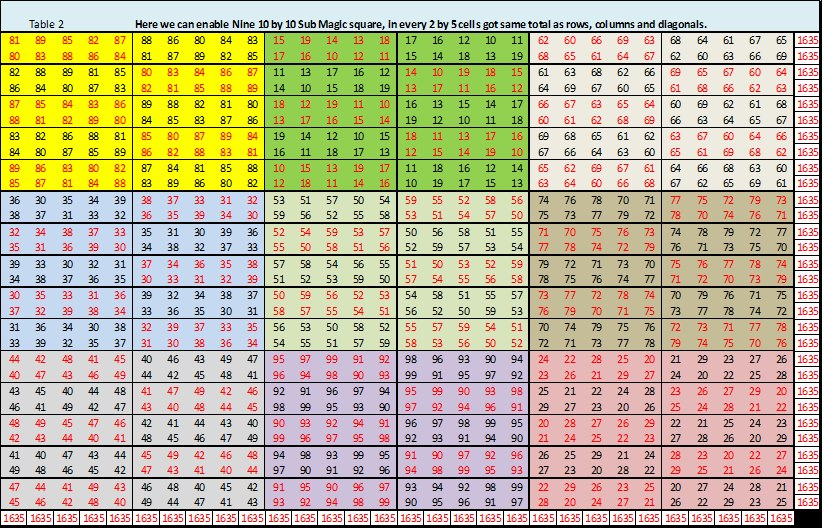
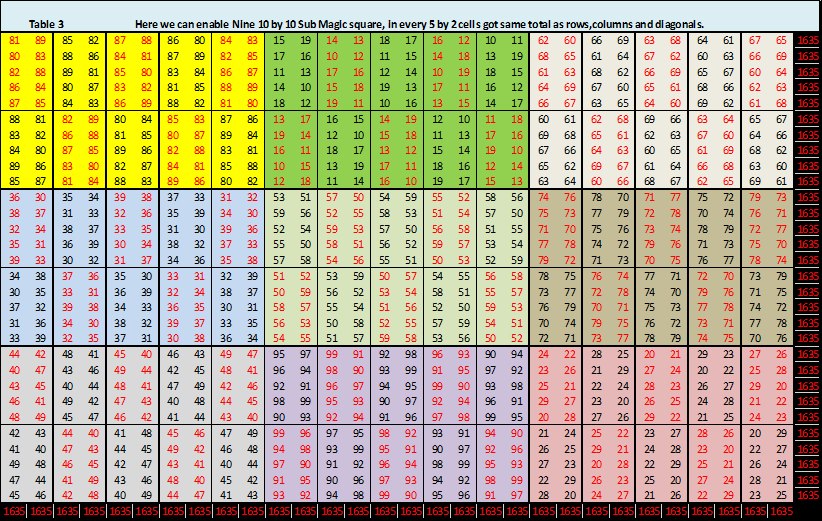
Similarly, we did all remaining 8 digits. So that 3 by 3 Magic square becomes Nine 10 by 10 Magic square or Latin square. Such that we can see a big 30 by 30 Magic square and the Magic constant is 1635.