Mathematical Matrix

16 X 16 Prime Reciprocal Magic Square

A 18 * 18 Magic square has long been known, we present here a procedure for generating a 16 * 16 Magic square may be for the very first time, using a very interesting method.

Let us start with 2 numbers A & B.

‘A’ is the reciprocal of prime number 17

A = 1/17 = 0.0588235294117647

Let us ignore the decimal point and write A as:  0588235294117647

B = 123456787654321 is a 15 digit palindrome number (Considering the digits on either side of ‘ 8 ‘).

We now adopt the following procedure:

1) Multiply A with B to get C_1,

       C₁ = 0588235294117647 * 123456787654321

——————————————————–

           072621639796659404502541902687

——————————————————–

Which is 30 digits long (including the leading ‘0‘)

2) Split C₁ equally into 2 parts, writing it down as,

*072621639796659

404502541902687+

Note that there is an offset or indent in the way the numbers have been written one above the other.

3) Add the two rows as written to get:

D₁ = 4117647058823529

Note that this result is similar to the number A, except that the last 7 digits in A are now the 1^st seven

and the 1^st 9 digits in A are now the last nine!

4) Now multiply D₁with a palindrome number ‘B’, and repeat the steps above. again, interactively.

I.e.  eg :  C₂ = D₁* B = 508351478576615831517793318809

Split these 30 digits again into two parts (as in step 2) to get

*508351478576615

831517793318809+

Add the two to get D₂ = 8823529411764705.

Note that D₂ again is similar to A, except there is a shift in the sequence!

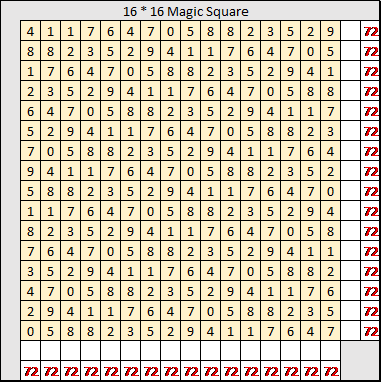
Repeat this procedure continuously, to get, in turn,

D₃, …D_4, …D₁₆.

These D_{i ,}  i = 1 to 16, when written top to bottom in sequence, form a 16*16 grid.

The sum of this 16*16 square along any column, row or diagonal, each yield the number 72!

This is a “Magic Square”

Email: Subramani.k@iiitb.ac.in