16 X 16 Prime Reciprocal Magic Square
A 18 * 18 Magic square has long been known, we present here a procedure for generating a 16 * 16 Magic square may be for the very first time, using a very interesting method.
Let us start with 2 numbers A & B.
‘A’ is the reciprocal of prime number 17
A = 1/17 = 0.0588235294117647
Let us ignore the decimal point and write A as: 0588235294117647
B = 123456787654321 is a 15 digit palindrome number (Considering the digits on either side of ‘ 8 ‘).
We now adopt the following procedure:
1) Multiply A with B to get C1,
C1 = 0588235294117647 * 123456787654321
——————————————————–
072621639796659404502541902687
——————————————————–
Which is 30 digits long (including the leading ‘0‘)
2) Split C1 equally into 2 parts, writing it down as,
*072621639796659
404502541902687+
Note that there is an offset or indent in the way the numbers have been written one above the other.
3) Add the two rows as written to get:
D1 = 4117647058823529
Note that this result is similar to the number A, except that the last 7 digits in A are now the 1st seven
and the 1st 9 digits in A are now the last nine!
4) Now multiply D1with a palindrome number ‘B’, and repeat the steps above. again, interactively.
I.e. eg : C2 = D1* B = 508351478576615831517793318809
Split these 30 digits again into two parts (as in step 2) to get
*508351478576615
831517793318809+
Add the two to get D2 = 8823529411764705.
Note that D2 again is similar to A, except there is a shift in the sequence!
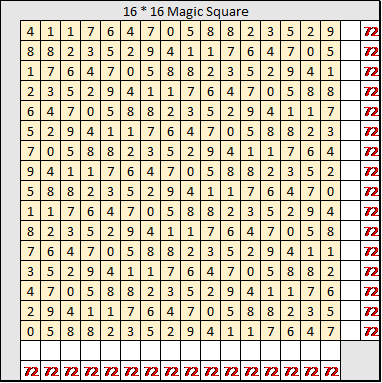
Repeat this procedure continuously, to get, in turn,
D3, …D4, …D16.
These Di , i = 1 to 16, when written top to bottom in sequence, form a 16*16 grid.
The sum of this 16*16 square along any column, row or diagonal, each yield the number 72!
This is a “Magic Square”
Email: Subramani.k@iiitb.ac.in


